Apparent Power and Power Factor

Today we went over all kinds of definitions of power regrading AC circuits. Unlike DC circuit, AC circuit has different values of voltage and current at different moments. Using the original definition for DC circuits on AC circuits only shows the instantaneous power. It does not tell us enough information about the circuit. Then we introduced the idea of effective voltage and current, which is equal to Vrms and Irms respectively.

We define apparent power as the product of Vrms magnitude and Irms magnitude. Since the voltage might be leading or lagging the current, there might be a phase difference between them. We represent the phase difference by using the power factor.

Since voltage and current have a real part and a imaginary part. We define complex power as the combination of both. The apparent power can be considered as the magnitude of the complex power, and the power factor is the cosine value of the angle. In rectangular format, the real term is called the real power, the imaginary term is called the reactive power.

Then we did a lab to test the new definitions of power. Here is a schematic of the circuit.

We applied different resistance values to the load resistor and measured them in the oscilloscope.

10Ω

47Ω

100Ω

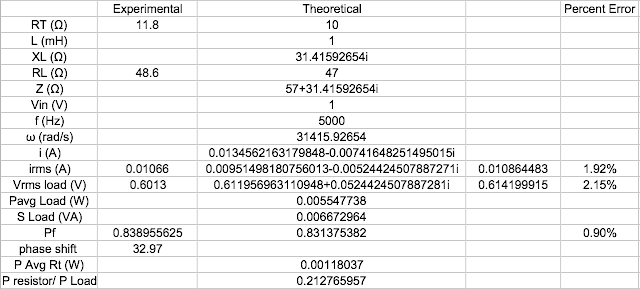
Then we compared the experimental values with theoretical values

10Ω

47Ω

100Ω

Summary: We concluded a list of useful formulas regarding power in AC circuits.

RMS Value of a Sinusoid
Vrms =Vp /√2 
Irms =Ip /√2

Impedance
Z = R + j X = |Z|∠θ
|Z| = (R2 + X2)1/2
θ = tan−1(X/R)
Note: θ is the angle of the load impedance (We have suppressed the subscript z.)

Ohm’s Law in Frequency Domain V = IZ
Vp = Ip |Z|
Vrms = V / √ 2
Irms =I/√2
Vrms = Irms |Z|
θv −θi =θ
θ > 0 when X > 0 (Inductive impedance) θ < 0 when X < 0 (Capacitive impedance)

Average Power (W)
P = Vrms Irms cosθ = Irms2 R = (Vrms2 cosθ)/|Z|

Power Factor
pf=cosθ=R/(R2 +X2)1/2, 1≥pf≥0.
If θ > 0 (inductive impedance), θi < θv, pf lagging 
If θ < 0 (capacitive impedance), θi > θv, pf leading 
If θ = 0 for purely resistive load and the pf is unity

Reactive Power (VAR) Q = Vrms Irms sinθ = Irms2 X
Apparent Power (VA) S=Vrms Irms =Irms2 |Z|=Vrms2 /|Z|
Complex Power (VA)
S=Vrms (Irms)*=Vrms Irms ∠θ=P+jQ=Irms2 Z=(Vrms)2/Z* 

Op Amp Relaxation Oscillator

Today we are introduced to a new circuit device called oscillator. An oscillator is a circuit that produces an AC waveform as output when powered by a DC input. In order to make an oscillator, the Barkhausen criteria have to be met. The overall gain must be unity or greater. Therefore, loss has to be compensated for by an amplifying device. The overall phase shift has to be zero.

The Wien-bridge oscillator is a common type of oscillator. It is an operational amplifier circuit with resistors and capacitors in it. It it limited to operating in the frequency range of 1MHz or less.

Then we did a lab to build a operational amplifying. Here is a schematic of the circuit

Here is the setup of the circuit

Summary: Oscillators can be used to convert DC signals to AC signals. It can be achieved by using operational amplifiers. The charge and discharge of capacitors of the circuit generate the alternating circuit signal.

Sinusoidal Circuit Analysis (No Lab)

Today we went over the circuit analysis methods that we used to solve DC circuits. Here is a list of all the methods.

The above methods still work in AC circuits as they work in DC circuits. Here are some examples of what we did in class.

Nodal Analysis

Mesh Analysis

Superposition

Source Transformation

Summary: Notice that superposition method is the only one that works for sources of different frequencies. When we turn off and on a different source, the impedances of capacitors and inductors have to be recalculated since they are frequency-dependent. All the other methods still work in AC circuits as long as frequency stays constant.

Impedance

Today we derived the impedance of resistor, capacitor and inductor. The impedance of a resistor is R; the impedance of a capacitor is -j/ωC or 1/jωC; the impedance of an inductor is jωL. It is obvious that the impedance of a capacitor or an inductor changes when different frequency is applied.

Impedance can be expressed as Z = R + Xj. Z is called impedance. R is called resistance. X is called reactance.

We also have the definition of their reciprocals. Y = G + Bj. Y is called admittance. G is called conductance. B is called susceptance.

Then we did a lab on impedance. We applied different frequencies to different types of circuit elements.

Resistor

R (Ω)	47
R0 (Ω)	100
Z (Ω)	147
f (kHz)	1
ω (rad/s)	6283.185307
Vin (V)	2
i (A)	0.01360544218
Vout (V)	1.360544218
Gain	0.6802721088
Phase Difference (º)	0

Capacitor 1kHz

R (Ω)	47
C (μF)	0.1
XC (Ω)	1591.549431	-90
Z (Ω)	1592.243258	-88.30849159
f (kHz)	1
ω (rad/s)	6283.185307
Vin (V)	2	0
i (A)	0.001256089477	88.30849159
Vout (V)	1.999128492	-1.691508405
Gain	0.9995642459
Phase Difference (º)	-1.691508405

Capacitor 5kHz

R (Ω)	47
C (μF)	0.1
XC (Ω)	318.3098862	-90
Z (Ω)	321.7610661	-81.60068958
f (kHz)	5
ω (rad/s)	31415.92654
Vin (V)	2	0
i (A)	0.006215792434	81.60068958
Vout (V)	1.978548182	-8.399310418
Gain	0.9892740911
Phase Difference (º)	-8.399310418

Capacitor 10kHz

R (Ω)	47
C (μF)	0.1
XC (Ω)	159.1549431	-90
Z (Ω)	165.9496789	-73.54761774
f (kHz)	10
ω (rad/s)	62831.85307
Vin (V)	2	0
i (A)	0.01205184616	73.54761774
Vout (V)	1.91811089	-16.45238226
Gain	0.959055445
Phase Difference (º)	-16.45238226

Inductor 1kHz

R (Ω)	47
L (mH)	1
XL (Ω)	6.283185307	90
Z (Ω)	47.4181233	7.614427915
f (kHz)	1
ω (rad/s)	6283.185307
Vin (V)	2	0
i (A)	0.04217796616	-7.614427915
Vout (V)	0.2650119773	82.38557208
Gain	0.1325059886
Phase Difference (º)	82.38557208

Inductor 5kHz

R (Ω)	47
L (mH)	1
XL (Ω)	31.41592654	90
Z (Ω)	56.53282622	33.75971669
f (kHz)	5
ω (rad/s)	31415.92654
Vin (V)	2	0
i (A)	0.03537767584	-33.75971669
Vout (V)	1.111422465	56.24028331
Gain	0.5557112325
Phase Difference (º)	56.24028331

Inductor 10kHz

R (Ω)	47
L (mH)	1
XL (Ω)	62.83185307	90
Z (Ω)	78.46554505	53.20247414
f (kHz)	10
ω (rad/s)	62831.85307
Vin (V)	2	0
i (A)	0.0254888945	-53.20247414
Vout (V)	1.601514474	36.79752586
Gain	0.8007572372
Phase Difference (º)	36.79752586

Summary: The impedance of resistors is independent from frequency. The magnitude of impedance of capacitors and inductors are related to the frequency. Larger frequency will cause the capacitor impedance to be smaller and the inductor impedance to be bigger. Smaller frequency will cause the capacitor impedance to be bigger and the inductor impedance to be smaller.

Phasors: Passive RL Circuit Response

We have completely finished the first part of the class, DC circuits. Now we move on to a new part of this class, AC circuits. Today we are introduced to a new powerful tool to analyze AC circuits, phasor. Phasor is a representation of a sinusoidal wave without the time dependence. Also, capacitors and inductors can also be considered as resistors with imaginary impedance. Ohm's Law still applies to AC circuits.

Then we did a lab on passive RL Circuit Response. Here is a schematic of the lab

We applied three different sinusoidal waves to the voltage input and calculated the gain and phase difference.

ω = 47krad/s

	Experimental	Theoretical	Percent Error
Angular Frequency (krad/s)	47.00	47.00	0.00%
Frequency (kHz)	7.48	7.48	0.00%
Gain	0.0149	0.015	1.28%
Phase Difference (º)	-43.1459	-45.000	4.12%

ω = 470krad/s

	Experimental	Theoretical	Percent Error
Angular Frequency (krad/s)	470.0	470.0	0.00%
Frequency (kHz)	74.8	74.8	0.00%
Gain	0.0021	0.0021	0.14%
Phase Difference (º)	-86.1859	-84.289	2.25%

ω = 4.7krad/s

	Experimental	Theoretical	Percent Error
Angular Frequency (krad/s)	4.700	4.700	0.00%
Frequency (kHz)	0.748	0.748	0.00%
Gain	0.021	0.021	2.89%
Phase Difference (º)	-4.933	-5.711	13.61%

Summary: The impedance of a resistor is R; the impedance of a capacitor is -j/ωC or 1/jωC; the impedance of an inductor is jωL. It is obvious that the impedance of a capacitor or an inductor changes when different frequency is applied. This causes the different gain and phase difference in each case. Using phasors can help us analyze AC circuits in the same way as DC circuits.

RLC Circuit Response

We are introduced to Schmitt Trigger. The primal function of the Schmitt Trigger, to convert noisy square waves, sine waves or slow edges inputs into clean square waves. One way to implement Schmitt Trigger is to use operational amplifier.

Then we did a lab on the step response of an RLC circuit. Here is a schematic of the circuit

We calculated the theoretical natural frequencies, undamped oscillation frequency, damped oscillation frequency and damping factor.

Here is the setup of the circuit

We calculated the damping ratio, DC gain, natural frequency, rise time and steady state response.

Damping Ratio	0.155
DC Gain	0.023
Natural Frequency (rad/s)	10105.823
Rise Time (ms)	0.622
Steady State Response (V)	0.046

Summary: Even though this RLC circuit is not a regular series RLC circuit, we can still use the same method to get the response. The difference is that the damping factor and undamped natural frequency would not be R/2L and 1/sqrt(LC). The correct α and ω0 can be found by using the characteristic equation. To get the characteristic equation, a typical way is to use mesh analysis or nodal analysis.